“El Arquitecto de los Números Naturales”

Este es un articulo inspirado en la Sección 2.1 de "Tao, Terence. Analysis I. 4th ed., Section 2.1, American Mathematical Society, 2016."

Giuseppe Peano (1858-1932) fue un destacado matemático y lógico italiano. Es famoso por sus cruciales contribuciones a la lógica matemática y la teoría de números. Nacido en Cuneo, Italia, Peano estudió y enseñó en la Universidad de Turín. Su legado incluye los axiomas de Peano, un conjunto fundamental de cinco axiomas que definen los números naturales mediante lógica de primer orden. Además, fue un pionero en el desarrollo de un lenguaje formal y la notación matemática, influyendo profundamente en la matemática moderna y la teoría de conjuntos.

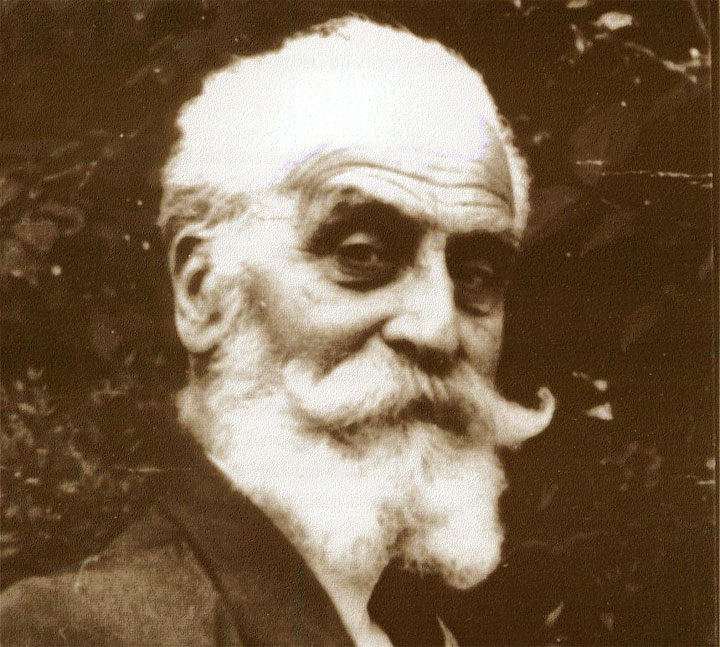
Los Cinco Axiomas de Peano:

• Axioma 1: 0 es un número natural.
• Axioma 2: Si nnn es un número natural, entonces n++ también es un número natural.
• Axioma 3: 0 no es el sucesor de ningún número natural.
• Axioma 4: Dos números naturales con el mismo sucesor son iguales.
• Axioma 5 (Axioma de Inducción): Si un conjunto contiene 0 y el sucesor de cada uno de sus elementos, entonces contiene todos los números naturales.

Contribuciones Clave:

• Reglas para los Números Naturales: Peano estableció una base lógica sólida para entender los números naturales. Este avance fue crucial para el desarrollo de las matemáticas.
• Lenguaje Matemático Claro: Peano fue pionero en promover un lenguaje matemático claro y preciso, lo que facilitó la comprensión y precisión en matemáticas.
• Mejora en la Notación: Además, mejoró la forma en que escribimos matemáticas. Su trabajo clarificó la notación matemática, facilitando el desarrollo del cálculo y otras áreas.

El legado de Giuseppe Peano sigue siendo fundamental en la matemática moderna, especialmente en la educación y la lógica matemática moderna.